This article will try and cover the topic about overhead line sag tension with calculation and example. If you belong to the electrical engineering world you must have questions regarding overhead line sag and tension. So, what do you know about sag?
What is Sag?
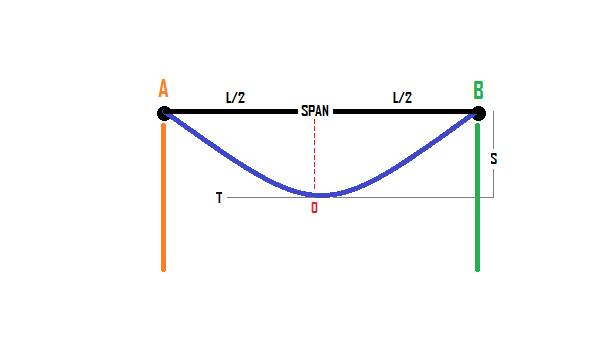
Before you get to know about sag, first learn how it is set up. An easy way to describe it is using an image. Suppose, A and B are two Points or you can also consider them two Transmission Towers. The vertical difference in level between the two points A & B (or, transmission towers) and the lowest point of the conductor is also what we can define as sag. The span of the overhead conductor affects the computation of sag and tension in a transmission line.
Some design engineers assume that the curve is parabolic for ease of analysis. The parabolic approximation is true only when the sag is minimal in comparison to the span length. It is common on distribution lines. Despite the complication of the formula, it is always advisable to use catenary calculations.
Catenary Curve
If the lowest point of the curve above is the origin, the following equation can also be in use to model it:
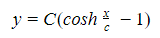
where:
- x = horizontal distance from span’s lowest point (m)
- y = vertical distance from the span’s lowest point
- C = Catenary constant
The catenary constant is effectively the ratio of the horizontal tension in the conductor to the unit weight in the absence of wind.
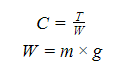
where:
- T = Horizontal component of tension (N)
- W = distributed load on conductor (N/m)
- m = unit mass of conductor (kg/m)
- g = gravitational constant of 9.81 m/s2
Overhead Line Sag Tension with Calculation and Example
When estimating sag in a transmission line, there are two conditions:
- When all of the supports are at the same level
- When support levels are not at the same level
The formula for calculating sag changes depending on whether the support levels (i.e., the transmission towers holding up the overhead conductor) are at the same level or not.
The sag calculation for supports is set to equal levels.
Sag Calculation at equal levels:
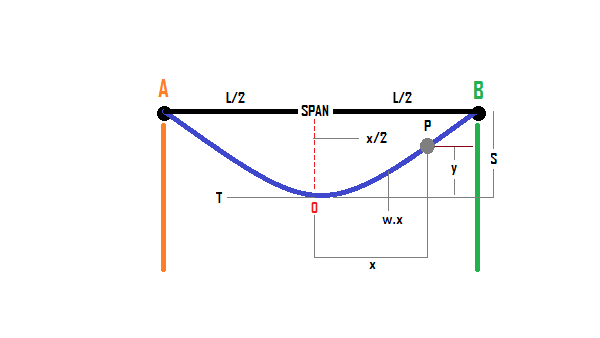
Assume AOB is the conductor. A and B are the support points. Point O is both the lowest and the midpoint.
Let, L denote the length of the span, i.e. AB
w is the conductor’s weight per unit length.
T denotes the conductor’s tension.
We’ve chosen any point on the conductor, let’s say P.
The distance between point P and the lowest point O is x.
y is the distance between points O and P.
We get by equating the two forces at the point O in the image above,
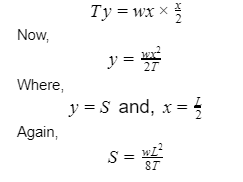
Sag Calculation at unequal levels:
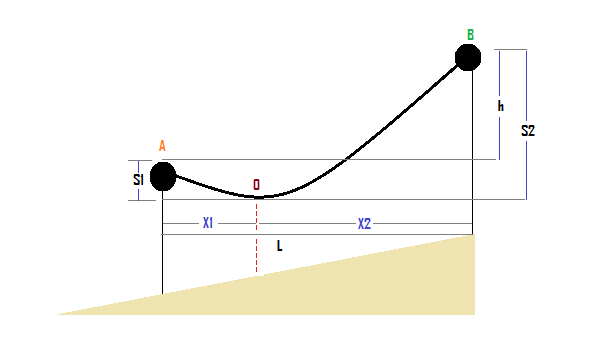
Assume AOB is the conductor with point O as its lowest point.
L is the conductor’s span.
h is the height difference between two supports.
x1 is the distance between support at lower level point A and O.
x2 is the distance between support at upper-level point B and O.
T denotes the conductor’s tension.
The weight per unit length of the conductor is denoted by w.

Solving equation (1) and (2), we get,

So, now that we know the values of x1 and x2, we can simply determine the values of sag S1 and sag S2.
When the conductor is in still air and the ambient temperature is normal, the above formula can compute sag. As a result, the conductor’s weight is its own weight.
What Impact Does Ice and Wind Have on Sag?
Ice can take on a variety of physical shapes in the conductor. They are as follows:
- ice glaze
- ice rime
- soggy snow
When the conductor is subject to the wind, the total unit weight of the conductor increases. This causes the catenary curve to alter shape. Line design engineers must account for potential excessive loading in the area while calculating sag-tension.
Under these severe loading circumstances, the conductor and supports may fail. It may also exceed the electrical clearances that are necessary.
The following are some of the effects of ice and wind on sag:
- When the wind blows at a specific force on the conductor and ice forms around it, the weight per unit length of the conductor changes.
- There is alternation of the conductor’s self-weight per unit length horizontally in the direction of the airflow by the wind force.
- Ice loading causes the conductor’s self-weight per unit length to shift vertically downward.
- The conductor will have a resulting weight per unit length if wind force and ice loading are both present at the same time.
- With the ice loading downward direction, the resultant weight will form an angle.
Assume that w is the conductor’s weight per unit length.
The weight of ice per unit length is what we know as wi.
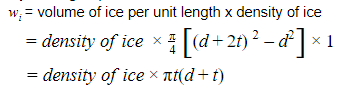
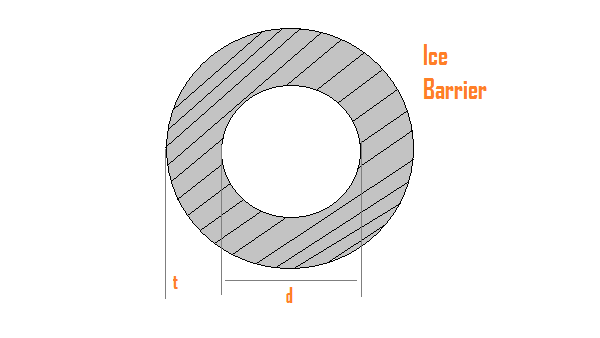
ww is the wind force per unit length.
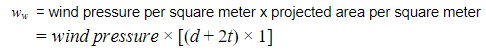
As a result, the conductor’s total weight per unit length is,
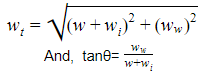
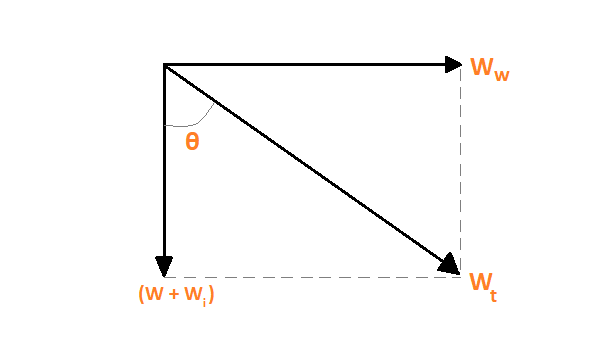
The conductor’s sag is achieved by,
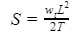
So, the vertical sag,
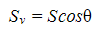
Why is sag in transmission line cables necessary?
The conductor’s sag determination is done by:
- Temperature
- Unit Weight of a conductor
- Deformation of Plastic (creep, strand settlement, etc.)
- Tension in the conductor Span Length
- The elasticity of conductor materials
- Weather Patterns (effect of wind, ice)
Consider the following important factors:
- A bent shape forms in the conductor due to the same two supports at the same level.
- In comparison to the conductor’s span, Sag is fairly small.
- The stress at the supports is almost equivalent to the tension in the conductor at any point.
- The Sag span curve has a Parabolic shape.
- Each conductor point’s stress always works tangentially.
- It will not exceed the tension limitations of the conductor under variable loading situations.
- Sag will be able to clear the necessary electrical clearances to the ground, and uplift.
- It will withstand the conductor tension if it can withstand the required amounts of electric and magnetic field, aeolian vibration, and ice galloping.
- The horizontal component of the conductor’s tension remains constant throughout its length.
Conclusion:
I hope you enjoyed my ultimate guide to overhead line sag tension with calculation and example.
Now I’d like to hear from you: do you know about overhead line sag tension? Do you like the way we did the overhead line sag tension with calculation and example?
Either way, let me know by leaving a quick comment below.
Read More Articles:

